
|
허수와 복소수에 대해서 알게 되면, 여러 가지 의문이 생기기 마련이다. 가장 먼저 떠오른다면, "복소수는 어디에 쓸모가 있을까?"일 것이다. 또 한가지를 들자면, "왜 하필이면 제곱해서 -1이 되는 수를 생각하나?" 일 수 있다. 이 두 가지 질문은 각기 별개로 가치 있는 의문이기도 하지만, 알고 보면 깊은 연관성이 있다. 한번 자세히 알아보자.
다른 방법으로 실수를 확장할 수는?

제곱하여 -1이 되는 수가 실수에는 없으므로, 이런 “가상의 수”를 도입하여 실수를 확장할 수 있다면, 다른 방법으로 실수가 아닌 수를 도입할 수도 있을 것이다. 예를 들어, 절댓값이 -1이 되는 수를 D라 하여 새로운 수를 만들 수도 있다. 이 경우 다음과 같이 여러 가지 문제를 생각할 수 있다.

이런 수끼리 연산이 가능할까?
1+D의 절댓값은 무엇으로 생각해야 할까?
D2은 실수일까?
확장된 수는 a+bD 꼴이 될까?

이와 같은 문제에 모두 합리적인 답을 할 수 있다면, 복소수와는 다른 새로운 수를 만들었다고 할 수 있다. 또, a2=1을 만족하면서 a≠±1인 수가 있다고 하여 새로운 수를 만들 수도 있다. 칸토어(G. Cantor)의 명언처럼 수학의 본질은 그 자유로움에 있기 때문에 아무리 해괴해 보이는 착상이라도 수학의 세계에서는 얼마든지 가능하다. 실제로 위의 두 예 모두 수학자들이 이미 생각해 본 착상들이다. 그렇다면 왜 이 새로운 수들은 복소수만큼 널리 알려지지 않았을까?
수학적 이론에 대한 판정 기준은 유용성

과학의 역사를 보면 세상의 온갖 현상을 설명하기 위해 다양한 이론이 개발되어 왔다. 그 가운데 어떤 이론은 대성공을 거두었는가 하면, 어떤 이론은 멋진 내용에도 불구하고 완전히 잊혀지기도 하였다. 일반적으로 새로운 이론이 인정을 받기 위해서는 "실험"이라는 검증 과정을 통과해야 한다. 아인슈타인의 상대성이론이 인정을 받은 것은 그 이론이 대단히 아름답기도 하지만 무엇보다도 수많은 실험을 통과하였기 때문이다. 수학의 경우는 어떨까? 순수한 사유의 산물인 수학적 이론의 경우, 물리학이나 화학의 "실험"과 같은 검증 과정을 거치지는 않으므로 그 자체로 논리적인 결함만 없으면 충분하다. 대신 어떤 수학적 이론이 널리 인정받는 데는 그 유용성이 가장 중요한 기준이 된다고 할 수 있다. 절댓값이 -1인 수나 ±1이 아니면서 제곱하여 1이 되는 수를 도입하여 확장한 수가 별로 알려져 있지 않은 것은, 이 새로운 수가 다른 문제를 해결하는 데에 별 도움이 되지 못했기 때문이다.
복소수의 기하학적 의미

복소수가 유용한 수학적 개념이 된 이유는 복소평면을 이용하여 기하학적 의미를 부여할 수 있었기 때문이다. 이를 통하여 평면기하의 여러 개념을 복소수를 써서 일관성 있게 설명하고, 또 새로운 개념을 무궁무진하게 이끌어낼 수 있었기에 - 심지어 복소수로 미분과 적분도 할 수 있다! - 복소수는 수학의 핵심적인 개념이 될 수 있었다. 복소수의 연산을 복소평면에서 어떻게 이해할 수 있는지 알아보자.
복소수의 덧셈
두 복소수 a+bi와 c+di의 합은 다음 그림처럼 평행사변형을 그려 그 대각선으로 나타낼 수 있다. 이것은 벡터의 합과 같은 방식이다.
복소수의 절댓값

| |

복소수의 덧셈(좌), 복소수의 절댓값(우)

|
복소수의 곱셈
두 복소수 a+bi와 c+di의 곱은 (a+bi)(c+di)를 분배법칙에 따라 일일이 전개해서 구할 수 있다. 그 결과는 (ac-bd)+(ad+bc)i이고, 이 결과를 복소평면에 그려 보면 다음과 같은 복소수가 된다.

곱의 절댓값 = 두 복소수의 절댓값의 곱
x축 양의 방향과 이루는 각도 = 두 복소수가 x축 양의 방향과 이루는 각도를 더한 것

그림에서 a+bi의 절댓값을 r1, x축의 양의 방향과 이루는 각도를 θ1이라 하고, c+di의 절댓값을 r2, x축의 양의 방향과 이루는 각도를 θ2라 하면, 곱의 절댓값은 r1 r2가 되고 x축의 양의 방향과 이루는 각도는 θ1+θ2가 된다.
회전변환
만약 절댓값이 1인 복소수를 곱한다면, 원점에 이르는 거리는 변하지 않은 채, x축과 이루는 각도만이 변하게 되므로, 복소수를 곱하는 것을 회전변환으로 해석할 수 있다. 예를 들어, 허수 단위인 i를 곱하는 것은 시계반대방향으로 90˚를 회전하는 것에 해당한다. | |
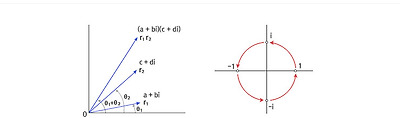
복소수의 곱셈(좌), 회전변환 (우)

|
삼각함수 공식
이런 기하학적 의미를 이용하여 유명한 공식 하나를 유도하여 보자. 절댓값이 1이고 x축 양의 방향과 이루는 각도가 각각 α와 β인 두 복소수는 cosα+isinα와 cosβ+isinβ이다. | |

cosα+isinα(좌)와 cosβ+isinβ(우)를 표시한 그림. 파란선의 길이는 1이다.

|
이 두 복소수를 곱하면 절댓값이 1이면서 x축 양의 방향과 이루는 각도가 α+β 인 복소수가 된다고 할 수 있다. 따라서 다음과 같은 결과를 얻는다.

실수부와 허수부를 비교하면, 두 각의 합에 대한 다음 삼각함수 공식을 한 방에, 그것도 동시에 두 개를 얻는다.

정확히 말하자면, 삼각함수의 이 두 공식 덕분에 복소수의 곱을 회전변환으로 생각할 수 있는 것이므로 앞뒤가 바뀐 셈이지만, 아무튼 고등학생들을 괴롭히는 대표적인 공식을 힘들게 외울 필요가 없다는 건 꽤 매력적이다. 다음에는 복소수의 제곱근이 어떤 기하학적 의미를 가지는지 살펴보고 이로부터 몇 가지 흥미로운 사실을 알아보자. | |












