피타고라스 정리

[귀뚜라미]

직각삼각형에 관한 피타고라스의 정리는 초등기하학에서 가장 아름다운 정리이자 가장 유용한 정리이기도 하다. 아래 그림과 같은 직각삼각형의 세 변의 길이 사이에 a²+b²=c²인 관계가 성립한다는 것이 피타고라스의 정리인데, 이것에 대한 확실한 논리적 증명을 처음으로 제시한 사람이 바로 피타고라스라고 알려져 있기 때문에 ‘피타고라스의 정리’라고 부른다.

피타고라스 정리는 고대인들도 이미 알고 있었다

그런데 여러 가지 증거에 의하여 이 정리는 피타고라스보다 약 1200년 전에 살았던 고대인들이 이미 알고 있었던 것으로 밝혀졌다. 고대 인도와 중국의 문헌에도 피타고라스의 정리가 소개되어 있으며, 피타고라스의 정리를 활용했다는 내용은 쉽게 찾을 수 있다. 특히 중국의 수학책인 [주비산경]에서는 이 정리가 ‘구고현의 정리’라는 이름으로 소개되고 있는데, 이 책에 수록된 구고현의 정리는 어떤 수식이나 기하학적 도해 없이 단 한 장의 그림으로 정리의 내용과 증명을 동시에 나타냈다. 그래서 파국이론의 창시자인 영국의 수학자 에릭 지만(Zeeman)은 구고현의 정리를 ‘세상에서 가장 아름답고 완벽한 증명’이라고 하였다. [주비산경] 제1편에는 오른쪽 그림과 함께 ‘구를 3, 고를 4라고 할 때 현은 5가 된다.’는 글이 있다. 중국에서는 구고현의 정리를 3000여 년 전에 ‘진자’라는 사람이 발견했다고 하여 ‘진자의 정리’라고도 부르는데, 이는 피타고라스가 이 정리를 증명한 것보다 약 500년 이상 앞선 것이다.

[주비산경]에 수록되어 있는 피타고라스의 정리에 관한 도해

피타고라스는 피타고라스 정리를 어떻게 발견했을까?

피타고라스의 정리는 피타고라스 이전에 이미 발견되었으며 역사에 기록된 증명법은 유클리드가 한 것이라는 견해가 있지만, 피타고라스에 관한 기록이 남아있지 않아 확실한 것은 알 수 없다. 그런데 만일 피타고라스가 이 정리와 증명을 발견했다면 이러했을 것이라 상상한 다음과 같은 두 가지 설이 있다.

1. 사각수로부터 얻었다는 설

1에서 홀수를 차례로 더하면 그 결과는 어떤 수의 제곱이 된다. 즉 이 성질이 발견되고, 피타고라스의 정리를 만족하는 가장 대표적인 세 수 3, 4, 5뿐만 아니라 5, 12, 13 그리고 7, 24, 25와 같은 경우에도 성립하는 것을 알게 되었을 것이라고 하는 설이다. 이 설은 어느 정도 일반성을 갖고 있지만, 직각삼각형의 변의 길이가 정수이고 빗변과 그 다음으로 긴 변의 길이와의 차가 1인 특수한 경우에 한한 것이었다. 이를 테면 9, 40, 41과 11, 60, 61 그리고 13, 84, 85는 모두 사각수의 성질을 만족한다.

2. 타일로부터 얻었다는 설

그 당시에 평면을 정다각형으로 깔려는 문제가 연구되고 있었다. 아래 그림에서 굵은 선으로 나타낸 부분을 보면 직각이등변삼각형에서는 피타고라스의 정리가 성립하고 있음을 알 수 있다. 이것으로부터 일반화한 것이 아닌가 하는 설이다. 그러나 직각이등변삼각형의 변의 길이의 비는 1:1:가 되어 무리수가 나오므로 이 설로부터 일반적인 경우를 얻었다는 것은 석연치 못하다. 오히려 정리를 발견하고 나서 이 정리를 직각이등변삼각형에 적용시켜 보고 무리수가 나와 곤란해졌을 것이라고 생각하는 것이 자연스럽다.

어째든 고대 작가인 플루타르크(Plutarchos)에 의하면 이 정리를 발견한 피타고라스는 매우 기뻐했고, 이 영광을 신에게 돌리기 위하여 소 100마리를 잡아 제물로 바쳤다고 전하고 있다. 논리학자인 아폴로도로스(Apollodorus)도 같은 주장을 하며, 다음과 같은 시를 남겼다. 사모스의 위대한 현인이 그의 고귀한 문제를 발견했을 때 100마리 황소들의 생혈이 땅을 적시었네. 그러나 당시 피타고라스는 영혼의 불멸과 윤회를 주장하고 있었으며 살육을 금지했고, 무혈제단을 권장했었기 때문에 신에게 바친 소는 진짜가 아닌 밀가루로 만든 소였다는 주장이 더 설득력이 있다.

피타고라스 정리의 증명

오늘날 피타고라스의 정리에 관한 증명은 약 400여 가지에 이르고 있으며, 이것에 흥미를 갖고 있는 사람들은 계속해서 새로운 증명법을 찾고 있다. 특히 루미스(Elisha S. Loomis)는 20세기 초에 피타고라스의 정리의 증명방법만을 모은 책을 발간했는데, 이 책에는 무려 367가지의 증명방법이 수록되어 있다. 피타고라스의 정리의 증명법 가운데 미국의 20대 대통령이었던 제임스 가필드(James Abram Garfield)가 발견한 방법은 재미도 있을 뿐만 아니라 수학적인 의미도 있다. 다음은 그의 증명 방법이다.

먼저 아래 그림과 같이 직각삼각형 ABC를 그리고, 이 직각삼각형과 합동인 직각삼각형 AED를 꼭짓점 A에서 겹치게 그린다. 이때 ∠BAD=90°가 되도록 한다. 그러면 사각형 CEDB는 밑변의 길이가 b이고 윗변의 길이가 a이면 높이가 a+b인 사다리꼴이 된다. 그리고 이 사다리꼴의 넓이는 다음과 같다.

그런데 이 넓이는 두 직각삼각형 ABC와 AED의 넓이에 한 변의 길이가 c인 정사각형의 반의 넓이를 더한 것과 같다. 즉, 다음과 같다. 따라서, 아래식이 유도된다. 이 식의 양변에 2를 곱한 후 양변에서 2ab를 각각 빼면 아래와 같다. 그러므로 직각삼각형에서 피타고라스의 정리가 성립함을 알 수 있다.

피타고라스 정리의 역, 피타고라스 3쌍 구하기

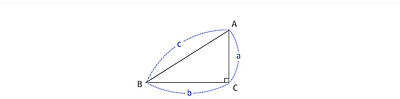
피타고라스의 정리는 그 역도 성립한다. 즉, 세 변의 길이가 각각 a, b, c인 어떤 삼각형이 a²+b²=c²을 만족하면 이 삼각형은 빗변의 길이가 c인 직각삼각형이다. 피타고라스의 정리와 그 역을 만족하는 세 정수 a, b, c의 쌍 (a, b, c)를 피타고라스 3쌍이라고 하는데, 가장 작은 수가 40 이하인 경우 피타고라스 3쌍은 다음과 같다. 

(3, 4, 5)	(5, 12, 13)	(6, 8, 10)	(7, 24, 25)	(8, 15, 17)
(9, 12,15)	(9, 40, 41)	(10, 24, 26)	(11, 60, 61)	(12, 16, 20)
(12, 35, 37)	(13, 84, 85)	(14, 48, 50)	(15, 20, 25)	(15, 36, 39)
(15, 112, 113)	(16, 30, 34)	(16, 63, 65)	(17, 144, 145)	(18, 24, 30)
(18, 80, 82)	(19, 180, 181)	(20, 21, 29)	(20, 48, 52)	(20, 99, 101)
(21, 28, 35)	(21, 72, 75)	(21, 220, 221)	(22, 120, 122)	(23, 264, 265)
(24, 32, 40)	(24, 45, 51)	(24, 70, 74)	(24, 143, 145)	(25, 60, 65)
(25, 312, 313)	(26, 168, 170)	(27, 36, 45)	(27, 120, 123)	(27, 364, 365)
(28, 45, 53)	(28, 96, 100)	(28, 195, 197)	(29, 420, 421)	(30, 40, 50)
(30, 72, 78)	(30, 224, 226)	(31, 480, 481)	(32, 60, 68)	(32, 126, 130)
(32, 255, 257)	(33, 44, 55)	(33, 56, 65)	(33, 180, 183)	(33, 544, 545)
(34, 288, 290)	(35, 84, 91)	(35, 120, 125)	(35, 612, 613)	(36, 48, 60)
(36, 77, 85)	(36, 105, 111)	(36, 160, 164)	(36, 323, 325)	(37, 684, 685)
(38, 360, 362)	(39, 52, 65)	(39, 80, 89)	(39, 252, 255)	(39, 760, 761)
(40, 42, 58)	(40, 75, 85)	(40, 96, 104)	(40, 198, 202)	(40, 399, 401)

고대 그리스의 위대한 수학자 유클리드는 위와 같은 피타고라스 3쌍을 구하는 방법을 얻었는데, 임의의 정수 m, n(m>n)에 대하여 a=2mn, b=m²-n², c=m²+n²이라고 하면 a²+b²=c²이므로 (a, b, c)는 항상 피타고라스 3쌍이라는 것이다. 예를 들면 m=4, n=2이면 피타고라스 3쌍 (12, 16, 20)을 얻는다. 하지만 유클리드의 방법으로 모든 피타고라스 3쌍을 구할 수 있는 것은 아니다. 이를테면 (9, 12, 15)은 유클리드의 방법으로는 얻을 수 없는 피타고라스 3쌍이다. 따라서 위에 제시한 피타고라스 3쌍 가운데에는 유클리드의 방법으로 구할 수 있는 것과 그렇지 않은 것이 섞여 있다. 어느 것이 유클리드의 방법으로 구할 수 있는 것인지 여러분들이 한 번 찾아보기 바란다.

글 이광연 / 한서대학교 수학과 교수