초월함수 미분

[귀뚜라미]

미적분의 개념을 넘어 응용을 몇 가지 더 소개하는데, 그를 위해서는 아무래도 간단한 함수 몇 가지를 미분하고, 적분하는 법을 알아야 할 것 같다.

다항함수의 미분법

[접선을 구하라-미분]편에서 썼듯이 f(x) = x² 의 x=L 에서의 미분 계수는 f’(L)=2L 이었다. 이를 뭉뚱그려서 f’(x) = 2x 라 쓸 수 있는데, 이렇게 정의한 함수 f’(x) 를 f(x) 의 ‘미분’ 혹은 ‘도함수’라 부른다. 한 번만 더 연습 삼아 f(x) = x³ 의 미분 계수를 구해 보면 다음과 같다.

즉,  x³ 을 미분하면 3x² 이란 얘기다. 이 정도면 패턴이 보일 것인데, 정말로 그렇다.

n 이 0 이나 음의 정수일 때도 성립하고, x>0 이라는 제한 조건을 단다면 n 이 유리수나 무리수여도 역시 성립하지만 증명하기 위해서 넘어야 할 산이 많다.

미분 가능한 함수 둘을 더해서 미분한 것은, 각각을 미분한 다음에 더한 것과 같다는 것을 극한의 성질을 써서 증명할 수 있다. 마찬가지로 미분 가능한 함수의 상수배의 미분도, 미분한 뒤 상수배하면 된다. 특히 다항식은 전부 미분할 수 있다. 예를 들어

xⁿ 을 미분하면  nx^n-1 이므로, 역으로 k 가 0 이 아닐 때 다음을 알 수 있다.

삼각함수의 미분 

미분 가능한 함수의 차, 곱, 몫 등의 미분법이나, 합성함수, 역함수의 미분법도 모두 알려져 있으므로 기본적인 함수만 미분할 줄 알면 못할 미분이 거의 없다. 이제 중요한 초월함수를 미분해 보자.

과거 수학 산책에 초월 함수를 미분하기 위해 암암리에 복선을 깔아뒀다는 걸 아시는 분은 아실 거다. 라디안을 설명한 글[각도의 단위-라디안]에서 사인 극한 정리를 언급했다. h 가 0 에 가까울 때, sin h 는 h 와 거의 비슷했다. 이를 식으로 쓰면 다음과 같은데 더 정확하게 증명할 수 있음은 물론이다. 위 식과 사인 함수의 덧셈 정리를 사용하면, sin x 의 미분이 cos x 임을 보일 수 있다. 마찬가지로 cos x 의 미분이 -sin x 라는 것도 보일 수 있는데, 여기서는 기하학적으로 설명해 보기로 한다. 원점이 중심이고 반지름이 1인 원 위를, 점 (1, 0) 을 출발하여 반시계 방향으로 길이가 t 만큼 걸어갔을 때의 좌표를 P (cos t, sin t) 라 부르기로 했다. t 가 변하면서 그리는 곡선은 원이다. 원과 접하는 직선은 접점과 원의 중심을 잇는 직선과 수직이어야 한다.

따라서 접선의 방향을 알려 주는 속도 벡터 ((cos t)’, (sin t)’) 는 그림에서 붉은색으로 그린 벡터 (-sin t, cos t) 의 상수배여야 한다. 그런데 속도 벡터의 크기가 1 이도록 움직이고 있으므로 상수는 1 이다! (반시계방향으로 회전하기 때문에 -1 이 아니다) 따라서, cos t 를 미분하면 –sin t 이고, sin t 를 미분하면 cos t 이다. 라디안을 도입하면 미분할 때 편하다고 했는데, 이는 원의 둘레를 속력이 1 이도록 움직이게 하는 각이 바로 라디안이기 때문이었던 것이다.

지수함수의 미분

e 의 출신을 설명한 글([자연상수 e – e의 출신은?])에서, t 가 0 에 가까운 수일 때 e^t 가 1차식 1+t 에 가까움을 설명했다. 즉, x=0 에서 y=e^x 에 그은 접선이 y=1+x 라는 뜻이다. 특히 f(x)=e^x 의 x=0 에서의 미분 계수는 이 접선의 기울기이므로 f’(0)=1 임을 알 수 있다. 즉, 다음 식이 성립한다.

따라서 아래와 같이 됨을 알 수 있다.

즉, 지수함수의 미분은 (e^x)'= e^x을 만족한다.

로그함수의 미분

y=e^x 위의 점 (a, b) 에서의 접선의 기울기는 b이다. b=e^a 이기 때문이다. 이 지수함수의 역함수를 y=ln(x) 라 쓰자. 역함수는 직선 y=x 에 대해 대칭이므로, 역함수 위의 점 (b, a) 에서의 접선의 기울기는 1/b 이어야 한다. 즉, y=ln(x) 의 도함수는  이다. 미적분의 기본 정리로부터  가 성립한다.

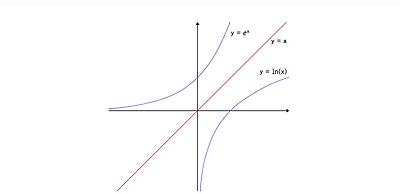
로그함수 ln(x) 는 e^x 의 역함수다. 즉, 직선 y=x 에 대해서 대칭이다.

급수와 미적분

위에서 배운 미분법을 이용하여, 멋진 급수를 하나 구해 보자. 첫째 항이 1 이고 공비가 -x 인 등비 수열을 n 개 더하면 다음을 얻는다.

양변을 구간 [0, 1] 에서 정적분하면, 다항 함수의 적분으로부터

임을 알 수 있다. 구간 [0, 1] 에서 y=1/(1+x) 의 그래프 아래쪽의 넓이는, 구간 [1, 2] 에서 y=1/x 의 그래프 아래쪽의 넓이와 같음을 알 수 있다. 따라서 로그 함수의 미분법에서

가 성립한다. 남은 적분 부분은

이므로 n이 클수록 0에 가까워진다. 따라서 다음 등식을 얻는다.

첫째 항이 1 이고 공비가  -x² 인 등비 수열을 생각하고 위와 똑같은 논법을 쓰면, 라이프니츠가 얻은 다음 등식이 나온다.

이 식은 라이프니츠(Gottfried Leibniz, 1646-1716)의 공식이라 부르는데, 실은 인도에서 마드하바 (Madhava, 1350 년경-1425 년경)가 이미 증명했다는 사실이 나중에 알려졌다.

미적분을 이용하여 정확히 구할 수 있는 무한합은 일일이 예를 들 수 없을 정도로 많다. 미적분을 통해 실수 및 함수에 대한 이해의 폭이 엄청나게 늘어나게 된 것이다. 특히 삼각함수나 지수함수, 로그함수 등을 이해하고 계산하는 도구로 미적분이 맞춤인 것도 알려졌는데, 그 이야기는 다음 회에 이어서 하기로 한다.

글 정경훈 / 서울대 기초교육원 강의교수