CAFE

전자계산응용C11

수치 해법에서의 오차

작성자한창호|작성시간15.09.03|조회수829 목록 댓글 0

 수치 연산의 오차


1) 절단 오차


테일러 급수(Taylor Series)는 다항식을 급수로 표현이 가능하다. 급수로 표현된 식은 무한으로 사용할 수 없어 결국 n차 이후 절단하면서 오차 Rn(x)가 발생한다.


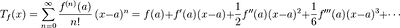
T_f(x)=\sum_{n=0}^\infty \frac{f^{(n)}(a)}{n!} \, (x-a)^n=f(a) + f'(a)(x-a) + \frac12f''(a)(x-a)^2 + \frac16f'''(a)(x-a)^3 + \cdots


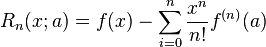
R_n(x;a)=f(x)-\sum_{i=0}^n\frac{x^n}{n!}f^{(n)}(a)


2) 반올림 오차


컴퓨터에서 실수는 간격이 있는데 가장 작은 간격을 머신 입실론(machine epsilon)이라 한다. 간격으로 인해 반올림 오차가 발생한다.


예)  1에다 0.00001을 만번 더하면 1.1이 나와야 하는데 1.100136이 나온다.


뺄샘할때도 반올림 오차가 생긴다.



3) 오차 최소화 방법

- 배정도 (double precision) 사용 (변수를 double 형으로 선언한다.)

- 그룹화 (나누어 더한다.)

- 테일러 급수 사용 (테일러 급수로 바꾸어 계산한다.)

- 뺄셈을 피한다.(tanh()를 exp()함수로 바꾸어 계산한다.)




지수 e


상수 e는 탄젠트 곡선의 기울기에서 유도되는 특정한 실수로 무리수이자 초월수이다. 스위스의 수학자 레온하르트 오일러의 이름을 따 오일러의 수로도 불리며, 로그 계산법을 도입한 스코틀랜드의 수학자 존 네이피어를 기려 네이피어 상수라고도 한다. 또한, e는 자연로그의 밑이기 때문에 자연상수라고도 불린다.


 

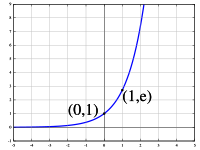
y=e^x  지수함수 그래프

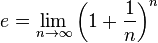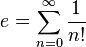
e = \lim_{n\to\infty} \left(1+\frac{1}{n}\right)^n  or  e = \sum_{n=0}^\infty \frac{1}{n!}


e는 무리수이기 때문에 십진법으로 표현할 수 없고 근삿값만을 추정할 수 있다. 소수로 나타낸 e의 근삿값은 대략 다음과 같다.


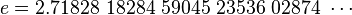
e = 2.71828\ 18284\ 59045\ 23536\ 02874\ \cdots


오일러 공식


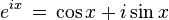
e^{ix} \,=\, \cos x + i\sin x


자연로그  - e를 밑으로 하는 로그인 자연로그이다.


f(x)=\ln x

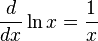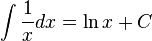
\frac{d}{dx} \ln x = \frac{1}{x} ,   \int \frac{1}{x} dx = \ln x + C


무리수


무리수(無理數)는 두 정수의 비의 형태로 나타낼 수 없는 실수를 말한다. 이에 반해 두 정수의 비에 의해 나타낼 수 있는 수를 유리수라 한다.


유리수

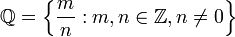
\mathbb{Q} = \left\{\frac{m}{n} : m, n \in \mathbb{Z}, n \ne 0 \right\}



테일러 급수 예


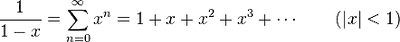
\frac1{1-x}=\sum_{n=0}^\infty x^n=1 + x + x^2 + x^3 + \cdots\qquad(|x|<1)

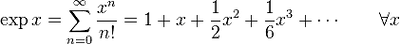
\exp x=\sum_{n=0}^\infty\frac{x^n}{n!}=1+x+\frac12x^2+\frac16x^3+\cdots\qquad\forall x

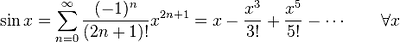
\sin x = \sum^\infty_{n=0} \frac{(-1)^n}{(2n+1)!} x^{2n+1} = x - \frac{x^3}{3!} + \frac{x^5}{5!} - \cdots \qquad\forall x

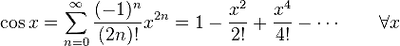
\cos x = \sum^\infty_{n=0} \frac{(-1)^n}{(2n)!} x^{2n} = 1 - \frac{x^2}{2!} + \frac{x^4}{4!} - \cdots \qquad\forall x

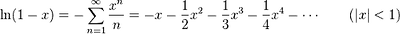
\ln(1-x)=-\sum_{n=1}^\infty\frac{x^n}n=-x-\frac12x^2-\frac13x^3-\frac14x^4-\cdots\qquad(|x|<1)

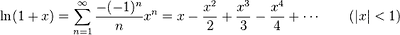
\ln (1+x) = \sum^\infty_{n=1} \frac{-(-1)^n}{n} x^{n} = x-\frac{x^2}2+\frac{x^3}3-\frac{x^4}4+\cdots\qquad(|x|<1)




참고: 첨부파일 1장-Taylor와 Maclaurin 급수.ppt



첨부파일첨부된 파일이 1개 있습니다.
다음검색
현재 게시글 추가 기능 열기
  • 북마크
  • 신고 센터로 신고

댓글

댓글 리스트
맨위로

카페 검색

카페 검색어 입력폼