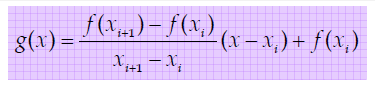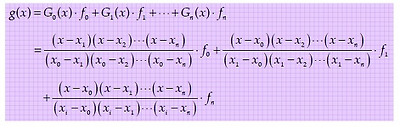Han's 카페

라그랑주 보간법 (Largrange's interpolation)

작성자한창호|작성시간15.09.10|조회수3,413 목록 댓글 0

선형보간법과 라그랑주 보간법의 차이

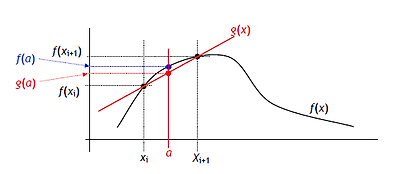
* 선형보간법

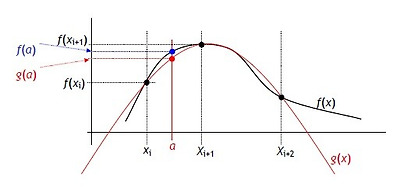
* 라그랑주 보간법

라그랑주 다항식은 라그랑주 형식에서 데이터 포인트의 주어진 집합으로부터 다항식을 보간하는 방법으로, 조제프루이 라그랑주의 이름에서 왔다. 이것은 1779년 에드워드 웨어링에 의해 처음으로 발견되었고, 1783년에 레온하르트 오일러에 의해 마지막으로 재발견되었다.

k + 1 데이터 포인트의 주어진 집합이 다음과 같이 있다.

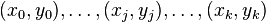
$(x_0, y_0),\ldots,(x_j, y_j),\ldots,(x_k, y_k)$

이때 라그랑주 형식의 보간 다항식은 다음과 같이 표현할 수 있다.

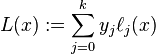
$L(x) := \sum_{j=0}^{k} y_j \ell_j(x)$

$\ell_j(x) := \prod_{f=0,\, f\neq j}^{k} \frac{x-x_f}{x_j-x_f} = \frac{(x-x_0)}{(x_j-x_0)} \cdots \frac{(x-x_{j-1})}{(x_j-x_{j-1})} \frac{(x-x_{j+1})}{(x_j-x_{j+1})} \cdots \frac{(x-x_{k})}{(x_j-x_{k})}.$

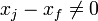
$x_j - x_f \neq 0$

이 그림은 네개의 점((−9, 5), (−4, 2), (−1, −2), (7, 9))에 대하여 (입방체의) 보간 다항식 L(x) (검정)을 보여준다. 이것은 크기가 변형된 기초 다항식 (y₀ℓ₀(x), y₁ℓ₁(x), y₂ℓ₂(x) 그리고 y₃ℓ₃(x))의 합이다. 보간 다항식은 4개의 모든 컨트롤 포인트를 지나고, 각각 크기가 변형된 기초 다항식은 그것들 각각의 컨트롤 포인트를 지나고 x가 다른 세개의 컨트롤 포인트에 부합되는 곳에서 0이다.