우리는 이 넓은 우주에서 혼자일까요?
아니 지금도 솔로인데 왜 또 혼자가 돼야 하나요?
- 시무룩
드레이크 방정식은 프랭크 드레이크 박사가 고안한,
우리 은하에 존재하는 외계문명 중에
우리와 교신할 가능성이 있는 외계 지성체의 수를 계산하는 방정식입니다.
N = R* x fp x ne x fl x fi x fc x L
이렇게 생겼습니다.
참고로, 드레이크 방정식은 푸는 사람마다 값이 다 다릅니다.
그리고, 이 문제를 하루종일 풀 수는 없으니까
간단 간단 하게만 짚고 넘어가도록 하죠.
또 이 계산에서는 태양계를 기준으로 방정식을 풀어나갈 겁니다.
혹시 외계에서 오신 분들 계시면, 고향별 기준으로 하시면 돼요.
마지막으로, 댓글로 직접 풀어본 답을 남기는 것도 굉장히 추천 드립니다.
그럼 하나씩 풀어볼까요?
우선 "R*"은 은하당 평균 별 생성률입니다.
그러니까, 1년마다 얼마나 많은 별을 만들어 내는지에 대한 값입니다.
보통 우리 은하 안에 존재하는 별들의 수를 별의 평균수명으로 나눈 값이죠.
우리 은하에는 별이 2,000억 - 4,000억 개 정도 있다고 해요.
저는 이 딱 중간으로 가겠습니다.
3,000억 개로 가죠.
3,000억 개 나누기 별의 평균수명 100억 년을 나눠주면, 30년이 나오죠.
R*은 30입니다.
"fp"는 별 중에서 행성을 가지고 있을 확률입니다.
지금 우리는 태양계를 기준으로 계산을 하고 있습니다.
태양만 한 별이 생성될 때 보통 행성계가 생기게 되지만,
이렇게 작은 항성들은 쌍성계를 이루게 됩니다.
쌍성계를 이루게 되면, 행성이 생성되기 어려운 조건이 되는데요.
바로 이 두 항성의 "중력적 섭동" 때문이죠.
중력적 섭동이란, 쉽게 이야기해서 천체의 궤도가 복잡해지는 걸 말합니다.
지구는 태양 하나를 공전하는데, 그 모양이 타원형에 가깝죠.
만약 태양이 2개라면, 이런 타원형이 아니라 조금 다른 모양일 겁니다.
그래서 궤도가 복잡해지니까,
행성이 공전하기 어려워지고, 생성되기도 힘들어지는 거죠.
어쨌든, 이런 쌍성계가 생기는 비율을 다시 50%라고 생각합시다.
어차피 인생 반반 무 많이 아니겠습니까!
놈당이구요.
이렇게 쌍성계가 생길 확률은 실제로 50% 정도 된다고 합니다.
그래서 "fp"의 값은 0.5가 됩니다.
"ne"는 행성계의 내의 생명이 살 수 있는 행성의 수를 말합니다.
그렇다면, 어떤 조건을 가지고 있어야 할까요?
우선 지구만큼 표면이 단단해야 하고,
적당히 에너지를 공급받는 행성이어야 하죠.
우리는 지금 태양계를 모델로 잡고 있으니까,
당연히 지구를 기준으로 계산할 겁니다.
우선 지구와 같은 기후를 가지기 위해서는
지구가 받는 에너지의 30% 이상을 넘기면 안 됩니다.
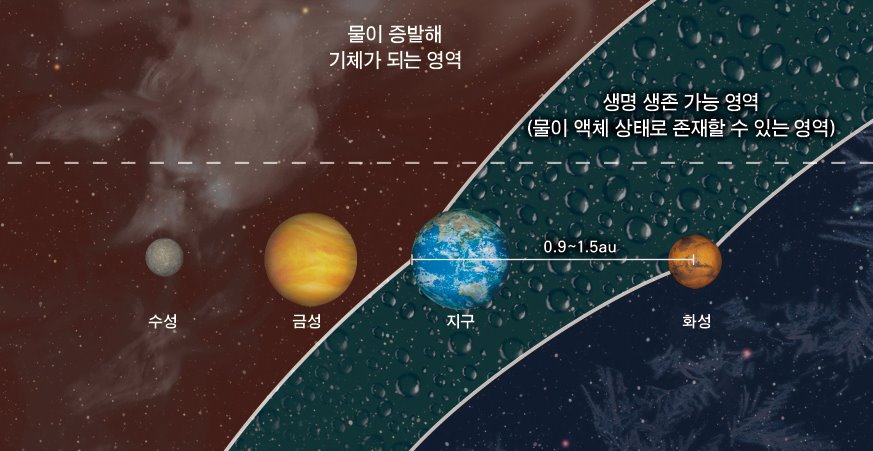
그러니까, 모항성과의 거리가 0.85 - 1.05AU 사이에 있어야 한다는거죠.
금성은 0.72AU 거리에 있고, 화성은 1.52AU 거리에 있습니다.
태양계에 지구 외에 생명체가 존재할 가능성이 있는 곳은 없다는 이야기죠.
어쨌든 우리는 "ne"의 값을 구해야 하니까 확률만 계산해봅시다.
우리가 구한 범위 0.85 - 1.05AU는 0.2AU의 범위를 가집니다.
여기에 0.2AU 나누기 40AU를 해주면 0.005라는 값을 얻을 수 있죠.
(*40AU는 태양의 중력이 미치는 거리 입니다.)
참고로,
"fp" x "ne" = 0.0025 라는 값이 나오게 되는데,
1년 동안 우리 은하에서 생성되는
생명체가 존재할 가능성이 있는 행성이 나올수 있는 값입니다.
1년에 0.0025개 젓갈만큼이나 짜죠
"fl"은 행성 내에서 생명이 탄생할 수 있는 확률을 이야기합니다.
여기서부터는, 굉장히 굉장하게 주관적인 값이 나오게 되죠.
말 그대로,
귀에 걸면 귀걸이
코에 걸면 코걸이
잠자는 친구의 코골이까지 되는 거죠.
-코 고는 소리
우리 태양계의 경우 8개 행성 중 단 한 곳 지구만 생명체가 있죠.
0.125 정도가 되는데, 사실 이렇게 많지는 않을 겁니다.
그래서 발견된 행성계 100군데 중에서 한군데 에서만 생명이 탄생한다고 가정하면,
0.125 x 0.01 = 0.00125라는 값이 나오죠.
너무 엉터리 아니냐구요?
아까 "인생은 반반 무 많이" 라고 했을 때부터 이미 엉터리였습니다.
넘어가죠.
- 뻔뻔
"fi"는 태어난 생명체가 문명을 가질 확률입니다.
이 값의 경우 무조건 문명을 가진다고 하면, 100%가 됩니다.
"1" 이라는 거죠.
이것 역시, 생명체가 태어난 행성 중
100곳에서만, 문명이 발생한다고 가정합시다.
우리 지구의 경우 11번의 대멸종이 있었던 것으로 예상되죠.
하지만 우리는 간단하게 계산해볼 거니까,
위에서 말한 데로 100곳 중 1곳에서만 문명이 생긴다고 가정합시다.
그래서 "fi"는 0.01이 됩니다. 1% 라는 뜻이죠.
"fc"는 이렇게 문명을 가진 외계 생명체가 우리와 통신할 수 있는 확률입니다.
우리의 경우 20세기 정도가 돼서야 우주에 신호를 보낼 수 있었죠.
그냥 문명이 아니라, 과학이 발달한 문명이어야 되겠죠.
이것 역시 계산하기 쉽게 0.01로 설정해 줍시다.
사실 이런 값들은 고려해야 할 게 너무 많고, 계산하는 방법도 너무 많습니다.
그래서 우리는 계산하기 쉽게, 간단 하게 가는 거로 합시다.
이로써, "fc"의 값은 0.01이 됩니다.
이제 마지막 "L"인데요.
"L"은 기술 문명이 존속하는 기간을 이야기합니다.
어떤 외계문명이 존재하는 시간을 이야기하죠.
종말은 아마도 모든 외계문명이나 우리 문명이나 피할 수 없을 겁니다.
언제 어떻게 멸망할지 예상할 수는 없지만, 지구를 기준으로 계산해 보죠.
인류의 첫 문명이라고 알려진 수메르 문명은
기원전 약 3,200년 전에 생겼다고 보죠.
이를 기준으로 3,200 + 2018
그리고 더도 말고 덜도 말고 이만큼만 유지된다고 가정했을 때,
10,436년이 되죠.
그래서 "L"의 값은 10,436년이 됩니다.
이제 모두 곱해보죠.
N = R*(30) x fp(0.5) x ne(0.005) x fl(0.00125) x fi(0.01) x fc(0.01) x L(10436) = 0.0000978375
30 x 0.5 x 0.005 x 0.00125 x 0.01 x 0.01 x 10436 = 0.0000978375 가 나옵니다.
우리 은하에 존재하는 교신이 가능한 문명의 수는
0.000098 개 라는 값이 나오죠.
3,000억 개의 별들 중에 문명이 있을 만한 행성이
0.000098개 밖에 되지 않는다는 겁니다.
그렇다면, 프랭크 드레이크가 제시한 외계문명의 수는 얼마나 될까요?
이건 프랭크 드레이크가 직접 사용한 값입니다.
N=R*(10) x fp(0.5) x ne(2) x fl(1) x fi(0.01) x fc(0.01) x L(10000) = 10
드레이크가 예상하기로,
우리 은하에 존재할 수 있는 문명의 개수는 10개였습니다.
댓글
댓글 리스트-
작성자26男의 무한도전 사랑 ♡ 작성시간 19.05.18 예전에 지식채널 e에서 한 번 이 내용을 본 적이 있는데, 이런 방정식이 있다는게 되게 신기하더라고요 !
-
작성자태권브이 V 작성시간 19.05.18 와 이런 게시글 너무 좋아요 ㅜ
-
작성자30꽃총각 작성시간 19.05.19 그냥 아 그렇구나정도일뿐 이건 이렇게 가정한다 처럼 저기들어가는 수식 대부분이 '그렇다 치고 혹은 이정도 될듯'이라면 수학적 측면에서의 확률로서 가치는 없는게 맞고 다만 이렇게 생각할 수 있지 않을까? 라는 부분에선 아주 좋은수식인듯 싶네요