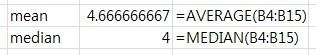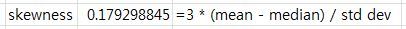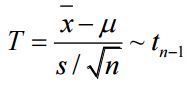12명의 환자에서 특정 다이어트 처방을 내린 후 2년 후의 체중 변화에 대한 데이터를 이용하여 처방이 효과가 있었는지 One Sample t Test를 하는 내용입니다.
0. 테스트 데이터 입력
1. One Sample t Test를 사용하기 위한 데이터의 조건
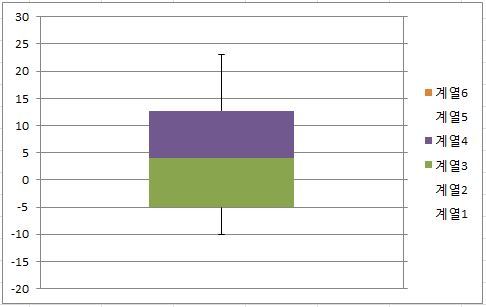
- median값이 boxplot의 중앙쯤에 위치할 것
- boxplot의 막대기인 whiskers가 위와 아래 방향으로 거의 같은 길이로 나와 있을 것
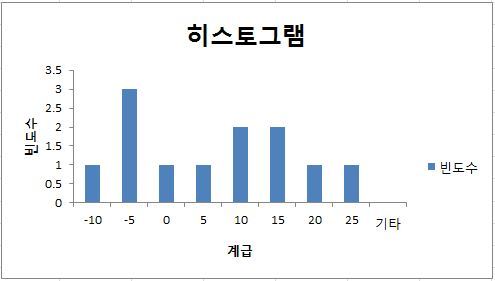
- histogram이 대칭으로 보일 것
- mean과 median이 거의 같은 것
- skewness(비대칭도)가 상대적으로 작을 것
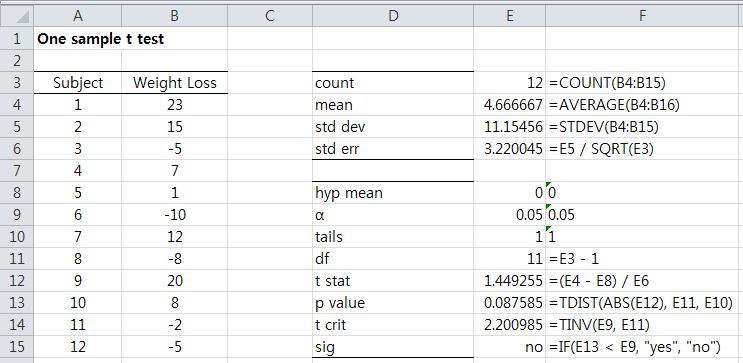
2. One Sample t Test
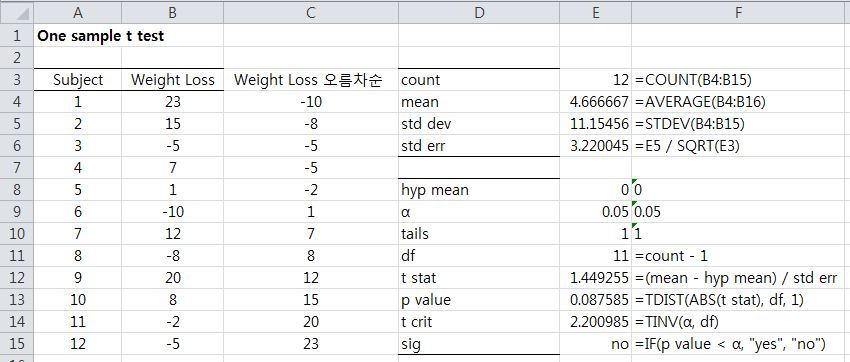
- 표본 데이터 추출 갯수(count), 평균(mean), 표준편차(std dev)를 이용하여 One Sample t Test를 위한 인자를 생성합니다.
- 처방에 따른 체중 변화가 없었다는 것이 귀무 가설이므로 hyp mean에는 0을 95% 유의수준이므로 α에는 0.05, right tail t-test이므로 tails에는 1, 자유도는 11이므로 df에는 11을 넣습니다.
- 추출 갯수(12), 평균(4.67), 표준편차(11.15)를 이용하여 t stat(1.45)를 구할 수 있습니다.
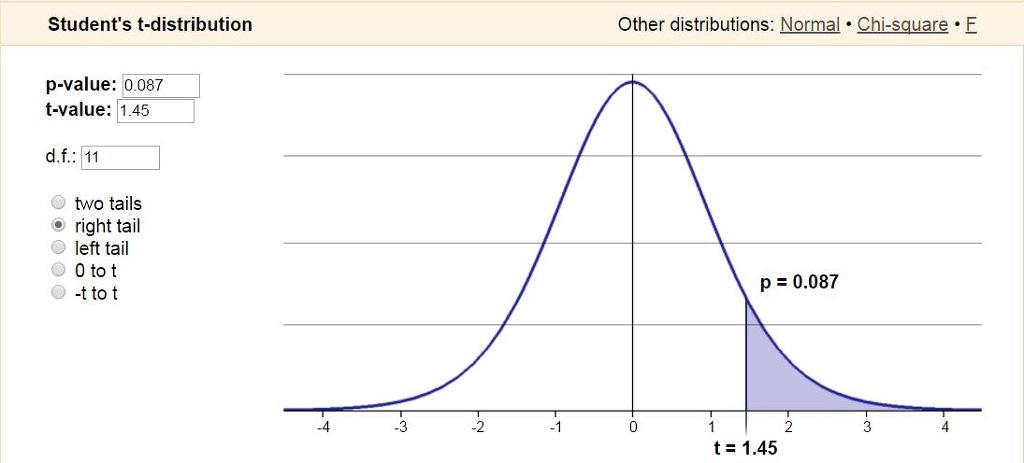
- One Sample t Test는 대부분 t stat를 p-value로 변환하여 보여주는데 이것을 시각화하여 볼 수 있습니다.
※ 그래프 링크 : http://www.statdistributions.com/t?t=1.45&df=11&tail=2
3. R에서의 One Sample t Test
# 데이터 입력
> data <- c(23, 15, -5, 7, 1, -10, 12, -8, 20, 8, -2, -5)
# 데이터의 정규성 검정
> shapiro.test(data)
※ p-value가 0.05 이상이므로 정규분포 가정을 만족
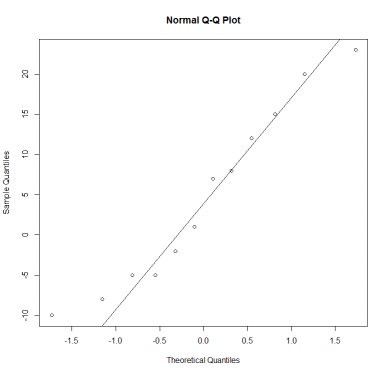
# 분위수-분위수 그림 Q-Q plot
> qqnorm(data); qqline(data)
※ 점들이 대각선에서 크게 벗어나지 않으므로 정규분포 가정을 만족
# mu에는 처방에 따라서 체중 변화가 없었다는 귀무 가설을 뜻하는 0을 넣습니다.
# alternative에는 right tail test를 의미하는 greater을 넣습니다.
# 유의수준은 95%가 기본값입니다.
> t.test(data, mu = 0, alternative="greater")
※ p-value값이 0.05보다 크므로 처방이 효과가 없다는 귀무 가설을 기각하지 못합니다.
4. One Sample t Test를 위한 Shiny App
- Shiny App 링크
http://shiny.stat.calpoly.edu/t_Test/
- Shiny App에서 사용할 샘플 데이터 CSV 파일
5. 엑셀 파일 첨부