1-1-4 관로 내 유체의 손실
1. 마찰에 의한 손실수두 (직선관로의 마찰손실수두)
직선관 속을 물이 흐를 때 관속의 압력은 하류로 갈수록 점점 떨어진다. 이는 관의 내벽면 마찰이나 점성에 의한 유체간의 마찰에너지가 소비되기 때문이다.
원관(圓管)의 마찰손실은 바이스바하ㆍ다르시(Weisbach & Darcy)의 실험식이 기본이지만, 다음의 하젠-윌리엄스(Hagen=Williams)식이 많이 사용된다.
ℓ ρv2
Δpf = λ ---- ㆍ ----
d 2
여기에서, Δpf : 압력손실[Pa]
λ : 관 마찰계수(그림 1.14의 무디선도로부터 구한다)
ℓ : 두 지점간의 직선거리[m]
d : 관의 내경[m]
ρ : 유체의 밀도[kg/m3]
v : 평균유속[m/s]
☞ 중력단위계
ℓ γv2
Δpf = λ ---- ㆍ ----
d 2g
여기에서, Δpf : 압력손실[kgf/m2]
γ : 유체의 비중량[kgf/m3]
g : 중력 가속도 = 9.8[m/s2]
에너지손실을 수두로 나타내면 그림 1.14처럼 단면이 일정한 수평관에 마노미터를 설치하여 측정할 수 있다. ①지점과 ②지점은 베르누이의 정리에 의해 위치수두ㆍ압력수두ㆍ속도수두는 각각 같은 셈인데 실제로는 ②지점의 압력수두는 ①지점보다 낮게 나타난다. 이 차이가 마찰에 의한 손실로서, 이것을 마찰손실수두(friction loss head)라 한다.
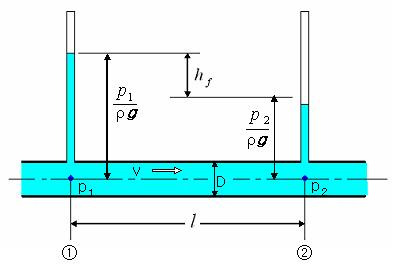
그림 1.14 직선관로의 마찰손실수두
p1 - p2 ℓ v2
hf = ----------- = λ ---- ㆍ ----
ρg d 2g
여기에서,
hf : 마찰손실수두[mAq]
p1 - p2 = Δp : 두 지점간의 압력차[Pa]
ρ : 유체의 밀도[kg/m3]
☞ 중력단위계
p1 - p2 ℓ v2
hf = ---------- = λ-----ㆍ ------
γ d 2g
여기에서, hf : 마찰손실수두[mAq]
p1 - p2 : 두 지점간의 압력차[kgf/m2]
γ : 유체의 비중량[kgf/m3]
위의 식에서 관마찰계수 λ는 관 내벽의 거칠기 ε와, 레이놀즈수 Re에 따라 정해지는 값으로서 무디(Moody)선도에서 구할 수 있다. 일반적으로 Re가 2,320이하인 층류의 경우는 거칠기에 관계없이 λ = 64/Re 이고, 난류인 경우는 관내벽의 거칠기에 많은 영향을 받고 있으나 개략 산정할 경우 λ = 0.03으로 한다.
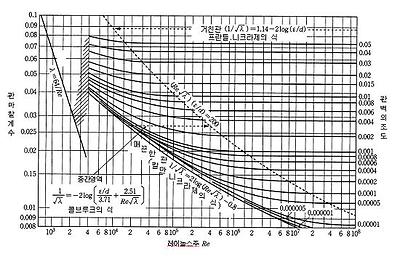
그림 1.15 무디선도
[예제 1-5] 호칭지름 25A의 배관용탄소강관(SPP)속을 매초 2[m]의 유속으로 물이 흐를 때 직선관 길이 10[m]당 마찰손실수두를 구하라. 다만, 마찰계수 λ는 0.03으로 한다.
(풀이)
호칭지름 25A SPP의 내경은 27.5[mm]이므로
ℓ v2 10 22
hf = λ ----ㆍ---- = 0.03 × ----------- × ----------- = 2.226[mAq]
d 2g 0.0275 2× 9.8
2. 국부저항손실
관로에 사용되는 밸브류, 이음쇠류 또는 관 단면의 변화 등에 의하여 생기는 손실을 국부저항손실이라 하며 다음 식과 같다.
ρv2
Δps = ξ ------
2
여기에서, Δps : 국부압력손실[Pa]
ξ : 국부압력손실계수
☞ 중력단위계
γv2
Δps = ξ -------
2g
여기에서, Δps : 국부압력손실[kgf/m2]
국부저항손실을 수두로 나타낼 경우는 다음과 같다.
v2
hs = ξ -----
2g
여기에서, hs : 국부저항손실수두[mAq]
위의 식에서 손실계수 ξ의 값은 국부저항을 받는 단면의 형상에 따라 다르며 일반적으로 실험에 의해 구한다.
복잡한 배관계에서 관이음이나 밸브류 등의 저항손실을 일일이 계산하는 것은 많은 시간이 소요되므로, 이들 국부저항손실을 동일 내경의 직관에서 발생되는 마찰손실수두에 상당하는 길이로 나타내면 편리하다. 이를 상당관 길이(등가관 길이 ; equivalent length)라 하며, ℓe로 나타내면,
ρv2 ℓe ρv2
ξ---- = λ---- ㆍ----
2 d 2
ℓe ξ
= ---- = ----
d λ
ξ
∴ ℓe = ---- ㆍd
λ
가 된다. 관로 전체의 압력손실Δp는 직선관로에서의 압력손실 Δpf와 국부압력손실 Δps와의 합으로서 다음과 같다.
Δp = Δpf + Δps
ℓ ρv2 ρv2
= λ ---- ㆍ---- + ξ----
d 2 2
ℓ ρv2
= (λ ---- + ξ) ----
d 2
ℓ+ℓe ρv2
= λ -------- ㆍ ----- [Pa]
d 2
☞ 중력단위계
ℓ+ℓe γv2
Δp = λ -------- ㆍ -------- [kgf/m2]
d 2g
☞ 마찰손실수두의 경우
ℓ+ℓe v2
hf = λ ---------- ㆍ ----- [mAq]
d 2g
표 1.2 국부저항 상당관길이(강관의 경우)
|
관의 호칭 지름 |
90° 엘보 |
45° 엘보 |
90°T |
90°T |
슬루스 |
글로브 |
앵글 |
임펠러 | |
|
mm |
B | ||||||||
|
15 |
1/2 |
0.6 |
0.36 |
0.9 |
0.18 |
0.12 |
4.5 |
2.4 |
3-4 |
[예제 1-6] 호칭경 50A의 강관으로 아래 그림과 같이 배관된 경우 A점에서의 압력이 0.3[MPa]일 때 B점에서의 압력은 얼마인가?
다만, 50A강관의 내경은 53.2[mm]이고 관내의 마찰계수 λ = 0.03, 유속 v = 2[m/s]이다.
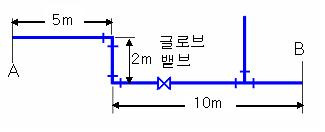
(풀이)
배관의 직선길이 : ℓ = 5+2+10=17[m]
상당관 길이 : ℓe =엘보(2.1× 2)+글로브밸브(16.5)+티(직류)(0.2)=21.3[m]
ℓ+ℓe ρv2
Δp = λ -------- ㆍ ------
d 2
17 + 21.3 1000× 22
Δp = 0.03 × ------------ × ----------- =43,196[Pa]=0.0432[MPa]
0.0532 2
∴ 0.3-0.0432=0.2568[MPa]