전에부터 두 지점 간의 거리를 직접 계산할 수 있으면 좋겠다는 생각이 있어 왔었는 데 이번에 시간을 내어 계산식을 찾고 계산프로그램을 작성하여 그동안 궁금해왔었던 것에 대해 조사한 것입니다.
1. 계산체제
사용식은 Wikepedia에 나와 있는 식들로[1,2] WGS84 지구모형에 대한 것이며 구체적으로는 아래와 같습니다.
1.1 경도선상의 위도간의 거리
적도에서 위도 파이까지의 거리,
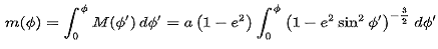
……1)
파이:위도[radian], a: 타원의 장반경=6378137.0 m e2: eccentricity제곱 =0.00669437999014
1.2 위도선상의 경도간의 거리
경도 1도 당의 거리, 파이:위도
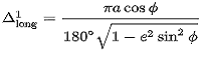
………………………2)
1.3 수식의 계산체제화
2)식은 바로 계산이 이루어질 수 있지만 1)식은 해석적 적분이 용이하지 않아 수치해석적 적분을 Excel내 VBA로 전산체제화
1.4 작성된 체제의 오차평가
가. 사용한 수식 제시처인 Wikipedia에 제시된 거리값과 비교:표시된 숫자 범위내 완전일치
나. MapSource와 Google Earth의 거리계산 값과 비교
.먼저 두 SW간의 일치성 평가: ~1500, ~2300km 떨어진 지점간의 거리들로 이 두 SW이 제시하는 거리의 숫자 갯수가 서로 다른 데 제시하는 숫자범위에서 서로 완전일치. 그래서 이들 값을 현실적인 참값으로 받아들여도 되는 것으로 판단
.동일 경도선상의 위도간 거리:MS,GE와 차이:0.0005%-10m(N25~N41의 2000km 계산시)
. 동일 위도선상의 경도간 거리:MS,GE와 0.1% 차이: 0.1%-3km(N25에서 2000km 계산시)(경도 차이값이 작으면 %오차가 줌)
. 서로 다른 경위도 두 지점간 거리:MS,GE와 0.07% 차이: 0.04%-0.6km(대만-서울 간 1500km 계산시)
오차는 계산이 더 복잡한 위도간 거리보다 비교적 간단한 경도간 거리에서 오히려 더 컸음. 그 이유는 2)식이 정확한 식이 아니라 간략식이기 때문이다? <-- 간략식 여부를 다음글인 2부에서 논의합니다.
그 이유는 어쨌든, 작성된 계산체제의 최대오차는 ~0.1%. 이를 감안하고 다음으로
2. 한국내 위치별 각도 거리
표1. 작성된 계산체제로 계산한 1도 차이에 따른 한국내 지역에서의 거리
| 거리,km/도 | (위^2+경^2)^0.5 | ||||
| 위도 | 위도차이 | 경도차이 | 대각선 차이 | 값 | 오차,% |
| 36 | 110.97 | 90.16 | 142.62 | 143.0 | 0.25 |
| 35 | 110.95 | 91.29 | 143.32 | 143.7 | 0.25 |
| 34 | 110.93 | 92.38 | 144.01 | 144.4 | 0.24 |
| 33 | 110.91 | 93.45 | 144.69 | 145.0 | 0.24 |
| 32 | 110.90 | 94.49 | 145.36 | 145.7 | 0.23 |
| 31 | 110.88 | 95.50 | 146.01 | 146.3 | 0.22 |
| 중앙값과 차이,% | 0.04 | 3.0 | 1.2 | ||
o 각 줄의 의미
- 위도차이: 동일 경도, 위도만 1도 차이되는 지점간 거리 o 각 줄의 의미
- 경도차이: 동일 위도, 경도만 1도 차이되는 지점간 거리
- 대각선차이: 경도, 위도 모두에서 1도씩 차이되는 지점간 거리
- (위^2+경^2)^0.5: 단순계산의 오차정도를 파악하기 위한 것으로 대각선 차이를 단순하게 직각삼각형의 변길이 정리로 '위도차이'와 '경도차이' 거리로부터 계산 한 값
위치에 따른 차이가 위도간 거리는 0.04%로 미미, 하지만 경도간 거리는 3%로 제법되고 있다.
3. 오차관점의 좌표계 필요 최소단위
그러면 좌표표시에서 발생되는 오차를 수용폭 이내로 하려면 좌표표기를 어느정도 상세히 해야 하는 건가의 답
조사 기준점:한국 중앙지역에 해당되는 N34 E128
표2. 각 각도차 별 거리
| 각도차,도 | 1 | 0.01666667 | 0.000277778 |
| 각도차 | 도, [km] | 분, [km] | 초, [m] |
| 1 | 1 | 1 | |
| 위도에서 차이 | 110.93 | 1.8857 | 33.277 |
| 경도에서 차이 | 92.385 | 1.5397 | 25.662 |
즉, 좌표표기 상의 오차를 1m이내로 줄이려면 표기를, 0.01초( 또는 3*10^(-6)도=소수점이하 6자리)까지 표기 필요
4. 통상사용되는 지도SW에서의 상황은?
조사대상 SW 중 Google Map은 한가지 단위체제만 제공하고 나머지 SW는 여러가지 단위체제를 제공하는 데 이들의 상황은 다음과 같았음
표3. 지도SW의 제공 좌표 단위체제와 최소 거리
| 지도 종류 | 표기 최소숫자 | 거리,m | |
| GPSMapedit | 도 | 1.E-06 | 0.1 |
| 분 | 0.001 | 1.9 | |
| 초 | 0.1 | 3.3 | |
| MapSource | 도 | 1.E-05 | 1.1 |
| 분 | 0.001 | 1.9 | |
| 초 | 0.1 | 3.3 | |
| Google Map | 도 | 1.E-05 | 1.1 |
| Google Earth | 도 | 1.E-06 | 0.1 |
| 분 | 0.001 | 1.9 | |
| 초 | 0.01 | 0.3 | |
즉, 좌표표시 상의 오차를 1m미만으로 하려면, '도' 단위체제를 사용하되 이들 SW 중에서 GPSMapedit와 Google Earth사용. 아울러 Google Earth의 '초' 단위 체계도 가능
5. 인용문헌
[1]. Latitude, https://en.wikipedia.org/wiki/Latitude
[2]. Longitude, https://en.wikipedia.org/wiki/Longitude
[* 이번에 사용한 식 중 위도간 거리식은 괜찮으나 경도간의 거리 식(2)는 정확한 식이 아니라 개략식으로 여겨지는군요. 경도간의 거리에 대한 정확한 식 자체나 찾을 수 있는 곳을 알고 있다면 이를 알려주면 고맙겠습니다.] <-- 삭제(21.3.10]
논의가 2부(https://cafe.daum.net/GPSGIS/Lrtt/1449)로 이어집니다
(*필요하다면 자유롭게 복사/스크랩 해가서출처를 밝히고서 잘 활용하세요. 흔적을 남겨주면 더욱 좋겠지요?)
댓글
댓글 리스트-
답댓글 작성자산타바 작성시간 21.03.09 나무 사용 용도가 무엇인지부터 확실히 하셔야 할 것 같네요. 대충 거리만 알려면 굳이 정확한 식이 필요 없을 거고 계산은 극히 간단합니다. 하지만, 측지학적 용도라면 vincenty 식이 맞습니다. direct는 거의 바로 구해지지만 inverse problem일 경우는 축차근사가 불가피하지만, 그렇게 많은 반복계산은 필요 없습니다. 엑셀로 시트 만들어도, 5-6회 반복시키면 mm 이상의 정확도가 확보됩니다(대척점 부근일 경우는 예외).
-
답댓글 작성자나무 작성자 본인 여부 작성자 작성시간 21.03.09 산타바 Wikipedia에 설명되어 있는 Vincenty 식의 적용상의 문제점이 실제는 그렇게 우려할만한 건 아닌가 보군요. Vincenty 식을 구체적으로 들여다 봐야겠네요 .필요한 정확성은 Google Earth나 GPSMapEdit 정도이면 됩니다. 언급했던 karney식의 논문이 찾아져 이것도 잠깐 훒어보았는 데, 혹시 식 적용에서 karney식과 Vincenty 식간의 상대적인 단순성, 계산상의 안정성에 대해서 언급해 줄 수 있는 지요?
-
답댓글 작성자산타바 작성시간 21.03.09 나무 본문 글에서 언급하신, 1식은 , "자오선호장"으로 불리는 것으로, TM투영법에서 중요한 식이며 많은 연구가 진행되어 있습니다. 위도의 급수전개방식으로 실무적으로 사용되며, 오차는 엑셀의 15자리 유효숫자 미만으로 구해집니다(실용상으로는 오차가 없다는 의미입니다). Vincenty의 논문을 보면, 대척점 부근에 대해서는 수렴속도가 급격히 저하되므로, 본인도 별도의 식을 제시한 것도 있습니다. vincenty식의 유용성(validation)에 대해서는 관련 논문들도 구글에서 찾으실 수 있으며, karney식은 더욱 높은 정확도를 주는식입니다(vincenty는 최대 0.1mm 단위이나 karney식은 pm 수준일 겁니다). 구글에서 쉽게 해당 논문을 찾아보실 수 있습니다.. closed form 형태의 식도 다른 연구자들이 제시하고 있으나 실제 활용하는 입장에서는 큰 의미는 없어 보입니다.
-
답댓글 작성자산타바 작성시간 21.03.09 산타바 2식은 근사식이 아니고, 정의(definition)의 문제입니다. 묘유선 곡률반경의 둘레/360도 한 식이므로 정확한 겁니다. https://en.wikipedia.org/wiki/Geographic_coordinate_system 위키의 이 항목중 length of a degree 마지막 문장 보세요
-
답댓글 작성자나무 작성자 본인 여부 작성자 작성시간 21.03.10 산타바 설명 덕분에 원했던 성격의 계산체제를 갖출 수 있게 됐네요. 고맙습니다. 그리고 마지막 댓글에서 언급했던 2)번식에 대한 것은 오늘 게시한 새 글에서 다루었습니다.