Q1. 정리7.2.3
"f : [a,b] → R 이 단조함수이면 f는 [a,b]에서 Riemann 적분 가능하다" 에서
리만적분의 전제조건인 'f가 [a,b]에서 유계'가 없어도 되나요?
f가 유계가 아닌 단조함수이면 리만적분이 정의가 되지 않는 것 아닌가요? ㅜㅜ
(아니면 단조함수이면 유계가 보장이 되나요..?)
Q2. 주7.2.2
아래 판서와 관련하여 질문입니다.
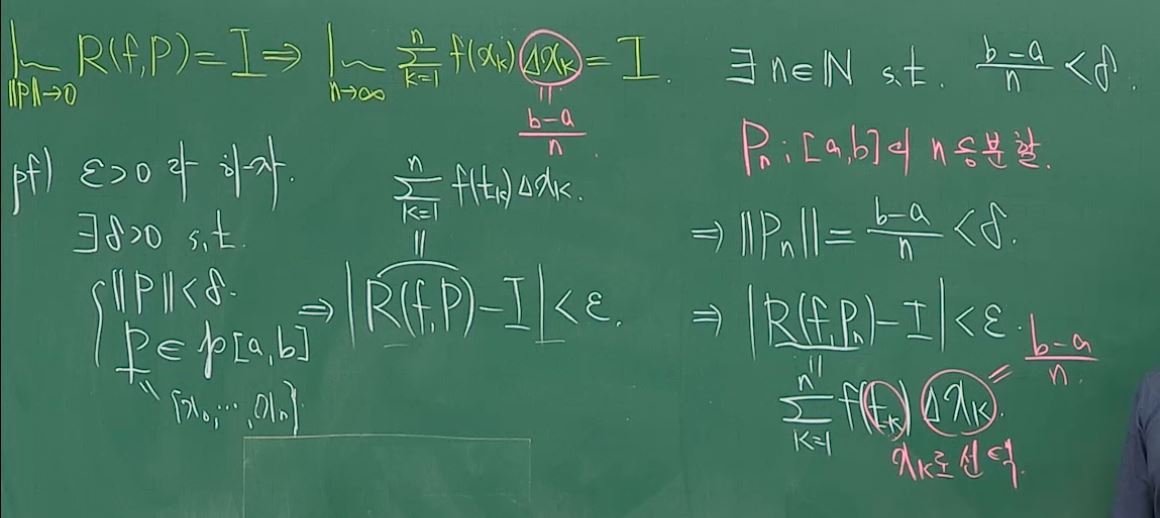


다음검색
댓글
댓글 리스트-
작성자김성희 작성시간 21.02.09 1. f가 [a, b]에서 단조함수이면 모든 x에 대해 f(a)≤f(x)≤f(b) or f(b)≤f(x)≤f(a)이므로 유계가 됩니다.
2. 뒷부분에 "m≥n이면 b-a/m ≤ b-a/n<δ를 만족하므로 m등분할 P_m도 필기 왼편의 성질을 만족하므로 풀어쓰면 m까지의 부분합과 I의 차의 절댓값이 ε보다 작아집니다."를 추가하면 증명이 끝납니다. -
답댓글 작성자PiXXeL 작성자 본인 여부 작성자 작성시간 21.02.09 아 헉헉,, 1번은 너무 당연했네요,, 감사합니다~~