[*중등경시*]기하문제

[offender]

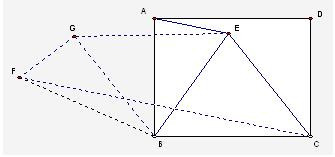
정사각형ABCD의 세 꼭지점 A, B, C에서 내부의 한점 E에 이르는 거리의 합의 최소값이 루트2+루트6 일 때 정사각형ABCD의  한 변의 길이를 구하시오.

점B를 중심으로 삼각형ABE를 60도 회전이동 한 것이 삼각형 BFG이고, 삼각형 BEG는 정삼각형이 되어 (선분AE)+(선분BE)+(선분CE)=선분(FC) 일 때 가 최소값 루트2+루트6 이 되는 경우라는데 왜 그렇게 되는지를 설명해주시면 감사하겠습니다.^^;

[수물화금짱]

AE+BE+CE에서 삼각형 ABE를 회전하였으므로 AE=FG,BE=BG인데요,각 GBE=60 이면서 BG=BE이므로 따라서 삼각형 BGE는 정삼각형 따라서 BG=GE 지금 까지를 종합하면 AE+BE+CE=FG+GE+EC 즉, 점F서 부터 점C까지의 이동거리를 뜻하는데 이동거리의 최소값은 직선,즉 선분이니까 CF일때 최소값이라는 거져..굳이 답까지 구하자면 각FBC=150, BC=BF=x 이므로 cos제 2법칙을 사용하면,x^2+x^2-2*x*x*cos150=CF^2 이때 CF=루트2+루트6이므로 대입하여 x값을 구하면 x=2 따라서 정사가형 ABCD의 한변의 길이는 2 가 답입니다.

[too lazy]

해설에 중등경시임을 감안하여 조금 덧붙이자면.. F에서 BC의 연장선에 내린 수선을 이용하여 특수각의 형태로 푸는 방법이 중학생이 이해하긴 더 좋을듯 하네요~

[수물화금짱]

아 중등경시였군요;;그래도 cos 제 2법칙은 알아두는것이 좋아요^^물론 기초가 필요하지만;;

[offender]

머릿속에서 정리가 잘 되질 않았는데... 일목요연하게 정리해 주셨네요. 감사합니다.^^;