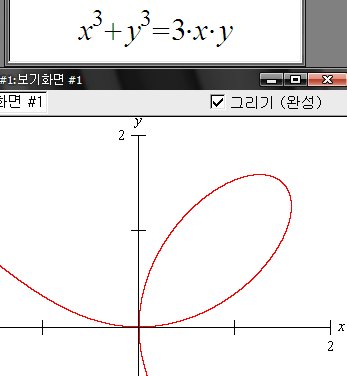
위와 같습니다. x^3+y^3=3xy 1사분면의 내부 넓이 구하는 방법.
면적분을 이용하면 될 것 같기도 한데. 매개변수변환을 어떻게 할 지 모르겠고...
그린 정리 써도 될 것 같기도 한데...
답답하네요.
어쨋든 답은 알고 있습니다. 9/2 입니다.
누가 좀 풀이 방법이라도 알려주세요~^^
다음검색
댓글
댓글 리스트-
답댓글 작성자세원군 작성시간 10.09.28 뭐.. 공대 1학년 답게 미적책에 있는걸 활용했어요 극좌표화 시켜서 넓이 구하기요. 그리고 적분 범위는 대충 θ=0과 다음으로 r=0이 되는 θ=π로 잡고요. 계산은 wolframalpha에 문의해봤는데 3/2가 나오더군요.
-
작성자세가지소원2 작성자 본인 여부 작성자 작성시간 10.09.28 우와~~이렇게나 많은 답이 달릴 줄이야~ 우선 답글 달고 생각해 볼께요~ 너무 감사해요~^^ 답은 틀렸을 수도 있어요~^^
-
작성자푸른하늘 작성시간 10.09.28 저도 아주 옛날 극좌표로 풀었던 문제같은데, 일단 답은 9/2가 아닌건 확실한게, 저걸 포함하는 아주 큰 사각형의 넓이도 4밖에 안되니까요~ ㅎㅎ
-
작성자세가지소원2 작성자 본인 여부 작성자 작성시간 10.09.28 맞아요. 9/2는 아닌 것 같네요. 윗 분들 말로는 3/2인 것 같긴 한데.....
근데 극좌표로 풀려면 r, θ 로 변수 변환 해야할텐데... 암만 조작해도 안되는 것 같아요. 혹시 r, θ 단일식이나 매개변수 표현 알고 계신 분 부탁드려요~^^ -
작성자세가지소원2 작성자 본인 여부 작성자 작성시간 10.09.28 맨 위엣분 덕분에 찾았어요~ 네이버에 '정엽선' 이라고 있네요.. 감사해요~^^