[초6문제]3문제좀 제발 도와주세용 ㅠㅠ..

[사화히하]

 직사각형 가 와 나 가 겹쳐져 있습니다. 겹친 부분의 넓이는 가 의 넓이의 3/4이고 , 나의 넓이는 2/5 입니다 직사각형 가 와 나 의 넓이의 비를 가장 간단한 자연수의 비로 나타내시오.

가  x 3/4 = 나 x 2/5   에요.

여기서  맨날먹는 밥님께서 설명해주고싶으신것은

ㅁ x 3 = ㅎ x 5 이니   두스를 같게하려면 ㅁ 에 5 를 ㅎ 에 3을  하면 둘다 같아지니.

2/5 : 3/4 = 2/5 x 20 : 3/4 x 20 = 8 : 15 

여기서요  왜     두 비를 자연수의 비로 만들고나서   8에 3/4 는 6이고  15에 3/5 =6 둘다 답이 같은데요.

왜 분수의 비를 자연수의 비로 만들어도 가튼지 궁굼해여 좀 알려주세요.

[2]

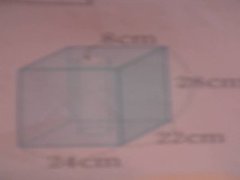
[가로 24 , 세로 22 , 높이 28 ]

오른쪽 입체도형은 직육면체에 밑면의 지름이 4cm 인 원기둥 모양의 구멍을 뚫은 것입니다. 이 입체도형의 부피를 구하시오.

여기서 요 24 x 22 = 528 한밑면의 넓이 의 x 높이 를 하면 부피를 구해지는데요.

여기서 한밑면의 넓이 에서 원의 넓이를 뺀후 곱하기 높이를 해서 부피를 구한 이유는 구멍이 뚤려서 그런가요 아 그냥 부피를 채우고 구멍은 신경 안쓰면 안되나 .ㅠㅠ    좀 알려주세요. 1cm3 가 가득차도 구멍은 별로 신경안쓸거가튼데 좀 알려주세요.

겉넓이  를 구할때요

밑넓이에서 구멍이 뚤어져 있으니 한밑면의넓이 - 원의넓이 를 한후에 구해진 답에 x 2 를 하면 밑면의 넓이가 구해지잖아요.

옆넓이를 구할때는요 24 + 22 = 66 x 2 = 132 x 높이 일텐데요.

132 + (4 x 3.14) x 28 이에요 이유가 머죠

왜 원의 넓이 까지 구해주는지 아닌가 4cm 라서 해깔려요 원의 넓이를 구할때하는건지. 원주 를 구할때하는건지 왜그런지좀알려주세요. ㅠ

[3]

가 물통에는 들이의 3/4 만큼, 나 물통에는 들이의 2/3 만큼 물이 들어 있습니다.

이 두개의 물통에서 같은 양의 물을 덜어내면 가 물통에는 들이의 1/2 만큼 , 나 물통에는 들이의 1/6만큼 물이 남는다고 합니다. 처음에 두 물통에 담긴 물의 양의 합이 39L 일때 , 나 물통의 들이는 몇L 입니까?

답을봐도 조금밖에 이해를 못하겠습니다. 설명좀해주세요 ㅠㅠㅠ..

[☆하늘지기이노☆]

겉넓이를 구할때에는 말 그대로 겉표면의 넓이를 구하는 겁니다. 입체도형의 안쪽에 원기둥의 옆면적도 곁표면에 포함되기 때문에 원기둥의 면적도 겉넓이에 포함되는 겁니다. 대신에 구멍이 뚫어져 있기 때문에 원의 넓이 위, 아래부분은 빠지게 되겠죠.

[☆하늘지기이노☆]

3번의 경우는 가의 물통을 x라고 생각하고, 나의 물통을 y라고 가정을 합니다. 그리고 나서 식을 세워보면 처음에 두 물통에 담긴 물의 양의 합이 39라 했으니 (x*3/4)+(y*2/3)=39라는 식을 하나 세울수 있구요. 두개의 물통에서 같은 양의 물을 덜어내면 가 물통의 1/2만큼, 나 물통의 1/6만큼 물이 남는다고 했으니 처음에서 나중의 물의 양을 빼면 가의 경우 3x/4-1x/2=1x/4가 되고, 나의 경우는 2y/3-1y/6=1/2가 됩니다. 즉 1x/4의 양과 1y/2의 양이 같게 된다는 말이죠.

[☆하늘지기이노☆]

x/4=y/2라는 식을 위에서 세운 (x*3/4)+(y*2/3)=39 식을 대입해서 계산하게 되면 x값과 y값을 구할수 있는데 여기서는 y 값만 구하면 되니까 y 값은 18L가 됩니다.

[사화히하]

하늘지기 님 직육면체 에서 밑면의 넓이는 원의 넓이를 빼서 구하죠 . 그런데요 여기서. 겉넓이를 구할때요 지름이 4cm 인 구멍이 있는데 밑면에 구멍을 뚫은 것인데요. 이걸 전개도로 피면 구멍 2개가 밑면에만 있을거 같은데. 높이가 일정하고 합동일거 뿐이고 구지 원의 옆면의 넓이를 구해준다는것이 이해가안가요. 부피도 마찬기지에요 밑면에만 구멍이 있을거 같은데. 겉넓이는 겉으로 혹은 밖으로 나온 것인데 . 이해가 안가요 설명좀해주세요 ㅠ.

[☆하늘지기이노☆]

지금 공간의 개념을 생각하셔야 하는데 너무 겉넓이 구할때 평면적으로만 생각하고 계신것 같아요. 위와 같은 입체도형 전개도로 만들려면 어려운데;; 사화히하님이 생각하시는 전개도대로라면 위 입체도형은 위와 아래를 잇는 통로부분이 생기질 않아요. 간단히 이해하기 쉬우시려면 지우개에 구멍을 뚫어놓고 한번 보시는게 빠를 듯 싶네요. 그러면 구멍이 뚫린 통로부분도 겉에서 보이기 때문에 그 부분의 넓이도 겉넓이에 포함되는 거에요. 그래서 원통의 옆넓이도 포함시키는 거구요.